I'm thinking to start off with this image*:
And the questions are - of course - What do you notice? What do you wonder?
I don't know which way it will go then.
But I know there are lots of great ways to go from this image. I'm hoping for some observations that are historical, and perhaps some mathematical ones.
One area I'd like to explore - historically and mathematically is the changeover from Roman numerals to Hindu-Arabic numerals. It could show us how a change in the way we think brings about changes in society. It could show us the importance of cultures outside Europe. And there's some potential great exploration of different number systems and numbers in different bases.
Already F has been writing some equations in Roman numerals, and R has been talking about how our system comes from India.
I like what Graeme Anshaw has done with this:
Starting a student-led inquiry maths unit (blogpost) http://t.co/p3SjUu51eI #ibpyp #inquiryed #pypchat pic.twitter.com/TcUuolSZAI
— Graeme Anshaw (@GraemeAnshaw) September 1, 2015
I think we'd probably want to get our heads round how Roman numerals work. Here's a good way:

Arithmetic wasn't so easy for the Romans, so they used a counting board or abacus:

It would be interesting to make, and try to use one of these. It looks like they work like a Japanese soroban:
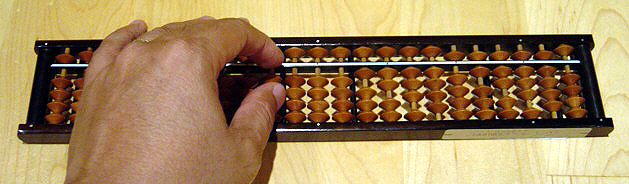 |
| source |
And then, how did they do this on a counter with jetons?
Here we could investigate other ways of representing numbers from different cultures, and at different times.
Now for Hindu-Arabic numerals...
 |
| source |
How did they make that journey, from India to the Muslim world, to Europe? Lots of stories in there, and I'm pleased there's such a strong cross-cultural element.
I've just been reading Keith Devlin's Man of Numbers, about how Fibonacci introduced them into Europe. There's lots worth finding out in that story too.
And thanks to Tracy, I have a nice little picture book about him to read and contemplate with the class:
Part of why this all seems more do-able to me now, is partly that I've seen there is lots of maths that can be explored by the students, rather than simply being told about. Reading Madeleine Goutard on our base system, and other bases, I see more clearly how we could represent them:
 |
| from Madeleine Goutard, Mathematics and Children |
The bottom one is perhaps how three-toed sloths might represent numbers, in base six.
 |
| Three-toed sloth (source: wikimedia) |
How about other bases? They could be represented by Dienes' blocks too:
 |
| source |
So, lots of directions to explore from that first image.
And then there's that dress, with that mysterious pattern of numbers.
See How We Wrote Numbers for reflections on how this went.
*Calculating-Table by Gregor Reisch: Margarita Philosophica, 1503. The woodcut shows Arithmetica instructing an algorist and an abacist (represented as Boethius and Pythagoras). There was keen competition between the two from the introduction of the Algebra into Europe in the 12th century until its triumph in the 16th. Source















 Hopefully, eg, that the two red angles are equal.
Hopefully, eg, that the two red angles are equal.































